Comparative methods, do we think we know more than we do?
Collaborators: Martin Lysy, Yoel Stuart
To correct a shortcoming in an approach taken by many, I am creating explicit and complete methods for estimating extinction and speciation rates using present day taxa.

This research is driven by my exposure to comparative methods, which is a rapidly growing field that attempts to infer characteristics about the historical evolutionary process using almost exclusively data from the present day. Studies in this field often come to rather firm conclusions, which is surprising given the scant amount of data available. Some of these conclusions are based on estimates of historical speciation and extinction rates, and we might ask, how can we estimate a rate per unit time when we can only observe one timepoint (the present?) and in particular, how could one possibly estimate an extinction rates if we never see a species go extinct?
Although there is every reason to be suspicious about conclusions from these studies, these suspicions do not necessarily mean that they are wrong, only that they cannot be trusted until the uncertainty around them is properly quantified. A quick review of the methods shows the problems in current attempts to do this. In a typical study, the researcher will sequence some small number of genes from a existing group of species, then will construct a phylogenetic tree based on these sequences, and finally will estimate parameters for some model of evolution using this tree and maximum likelihood (e.g. how phenotypes diverge through time, speciation rates, etc.). Models are frequently compared using AIC scores, with some researchers even assigning p-values to these.
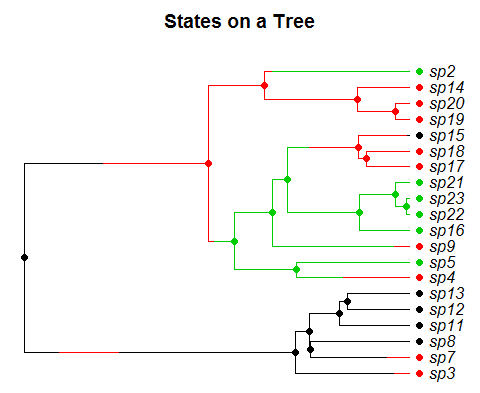
A tree simulated from the model we consider. Species evolve forward in time and exist in one of several states (represented by colors). Each state has a distinct speciation and extinction rate and species move between states according to a markov process. The goal is to estimate the rates in each state, and whether or not they are changing through time.
This general approach has a large number of shortcomings. Although it is a given that any approach to infer historical rates from only present day data must be heavily model dependent, we at least want to properly account for the uncertainty for a given model, which these methods fail to do. The most common error in these studies, and perhaps a reason they are able to generate firm conclusions with so little data, is that they suffer from the single imputation fallacy and assume to know things without error which are not known, most prominently the phylogenetic tree. Additionally, the data generating model for a given study is typically poorly, or not at all, defined, which makes correctly calculating the likelihood function impossible (a common example is calculating the probability of the root state on a tree). Finally, the model comparison strategies used are too simplistic, relying on asymptotics that quite possibly are not applicable. For example, the likelihood ratio test is often employed to support conclusions. The justification for the LRT as part of standard phylogenic inference is that a large number of independent sites in a sequence alignment are observed, which allows for the independent-identically-distributed criteria to be satisfied and the results to converge on the asymptotic distribution. However, in these datasets one often measures only one character and there is no independence, implying the asymptotic should be a very poor approximation. Similarly, it is well known that AIC scores can give very misleading results, particularly if all the models considered are wrong, but they can also mislead even if the correct model is considered and infinite data is available. Given these shortcomings, it appears ease of implementation has largely guided method choice. Separate software packages are available for each step in the analyses as they are currently done, and often no single unified software is available for a proper accounting of the uncertainty and covariance for the estimated parameters.
I am currently creating a method of inference that accounts for these issues and also am comparing results from this correct method to the existing "approximate" methods to assess what, if any, problems result from using these single imputation approximations. My method jointly infers all model parameters, is based on an explicit generative model and allows for model comparison without resorting to asymptotics. I am doing this with a case study of Caribbean anole lizards, which have radiated over the past several million years onto different islands, but for which no fossils or extinctions have been recorded. I am redoing an analysis which assumes that the lizards on each island evolve with distinct speciation and extinction rates that may change through time, which is a simple extension of the BiSSE model. Creating an integrated model presents a number of algorithmic difficulties, but progress is currently being made using both a missing data approach that simulates complete trees and scales to arbitrary sized datasets, and a more traditional numeric approach which attempts to calculate probabilities integrated across trees using numeric ODE solvers but which scales more poorly.
Although past work based on single imputations was a necessary building block in the development of complete models, I hope the development of more unified models will avoid conclusions that are not truly supported, or at the very least show why approximations used due to computational ease are, or are not, accurate.